本节将展开介绍 IHPA 相关的基本概念和一些具体使用细节。
如果你还不知道什么是 IHPA,可以先阅读介绍。
如果你希望快速上手使用 IHPA 的核心功能,可以跟随快速开始。
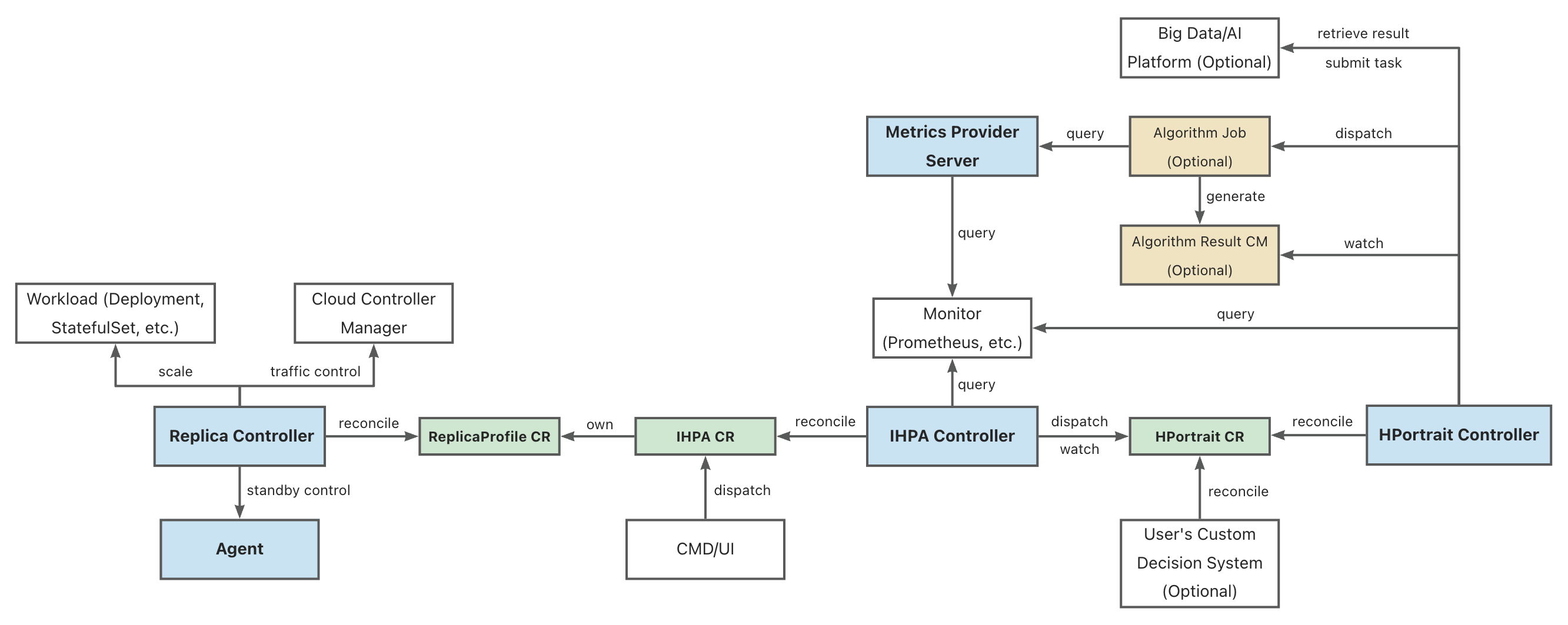
图例:
部分缩写的全称:
IHPA 执行层组件,负责具体工作负载副本数量和状态控制,其通过对接不同的原生和第三方组件支持 Pod 的扩缩容、摘挂流和激保活等操作。
IHPA 控制面组件,直接接受用户或外部系统的 IHPA 配置(包括目标工作负载、指标、算法、变更与稳定性配置等),下发画像任务并整合画像结果,再根据画像结果执行多级分批弹性伸缩。
内置水平弹性伸缩算法管理组件,负责运行和管理针对不同工作负载的不同弹性伸缩算法的工作流,并将其输出结果转换为标准画像格式。具体的算法子任务则会作为单独的 Kubernetes Job 或者其他大数据/算法平台的任务被调度执行。这些子任务会从外部监控系统中获取历史与实时指标数据进行计算并生成画像结果。
特别的,部分简单算法(如响应式算法等)的逻辑是直接实现在该组件中,不再走单独的算法子任务。
统一监控指标查询组件,屏蔽底层监控系统差异,为外部运行的组件(如算法任务等)提供统一监控指标查询服务。
其提供的 API 与 Kubernetes Metrics API 类似,但不同的是它能够同时支持实时和历史指标查询。
运行在 Kubernetes 集群节点上的 agent 组件,主要负责执行 Pod 的激保活等需要与底层操作系统进行交互的操作。
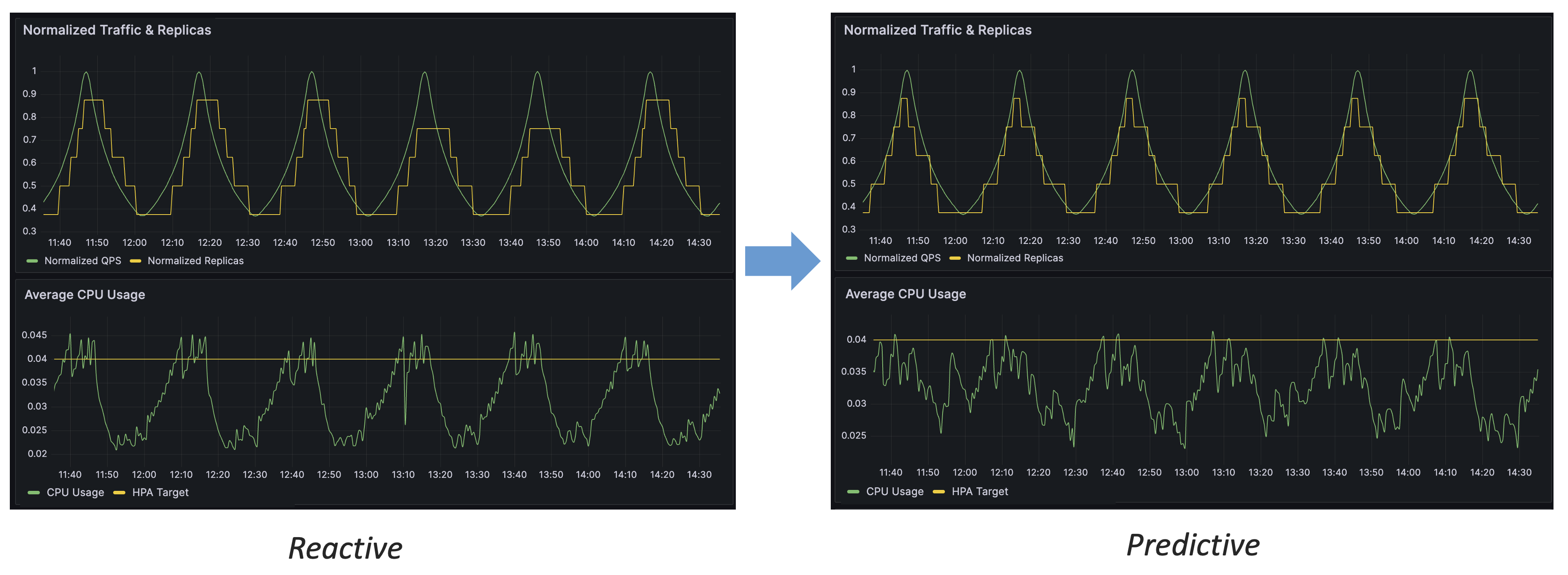
通过上图的对比,我们可以得出预测式扩缩容相比于响应式的几个优势:
下面将详细介绍 IHPA 的「基于流量驱动的副本数预测」算法的设计思路与工作原理。
对于在线应用来说,容量(资源)指标(如 CPU 利用率)与流量是强相关的,即流量变化驱动了容量指标的变化。我们通过预测流量来评估容量,而非直接对容量指标进行预测,会有如下的好处:
为了将副本数预测问题转化为流量预测问题,我们设计了一个 Linear-Residual Model 来找到流量、容量与副本数三者之间的关联函数,如下图所示:
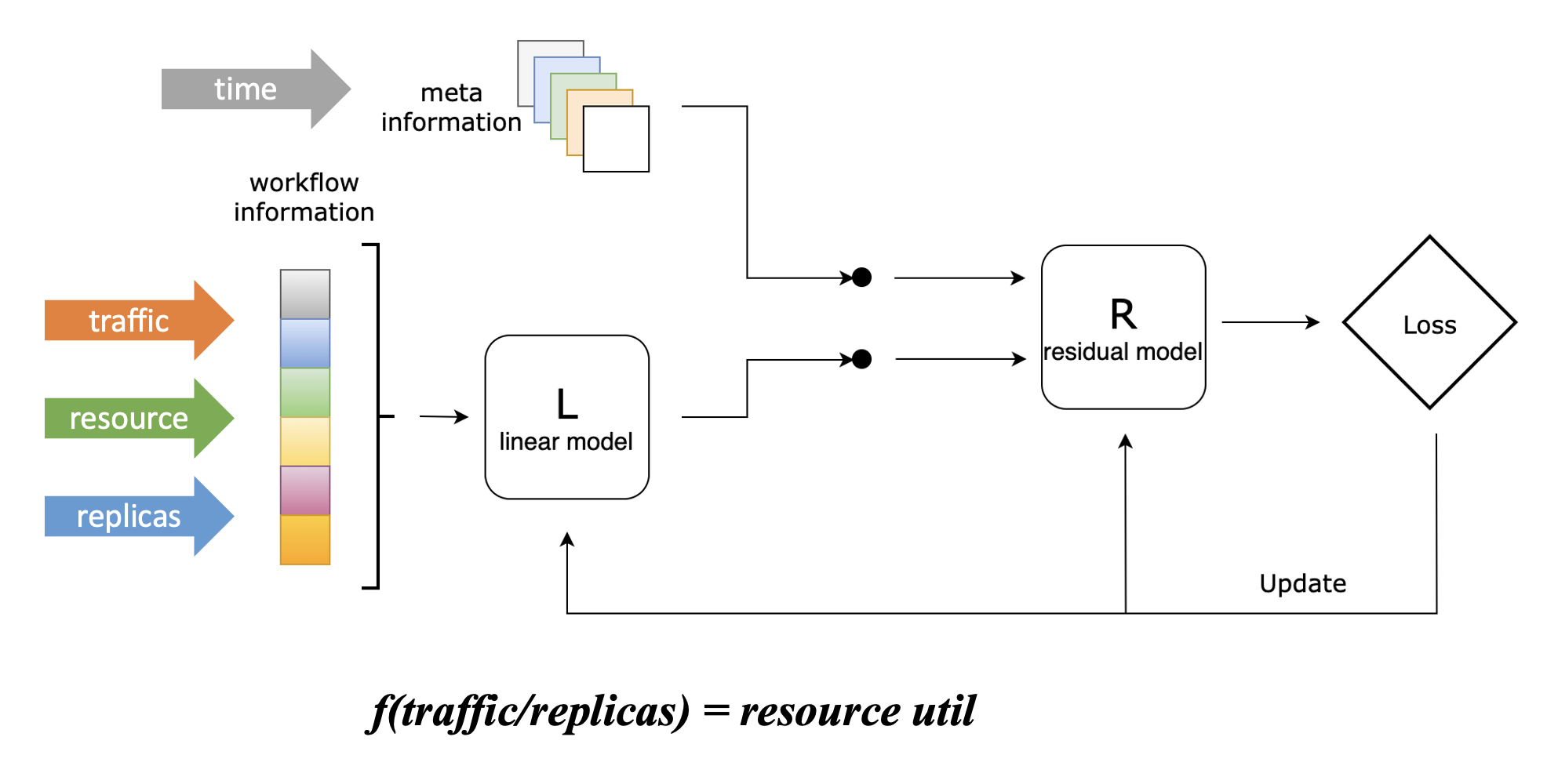
在该模型中,我们将资源利用率设置为目标指标,因为控制应用的资源水位是我们使用弹性伸缩的最终目的,这也是最符合直觉的。
但不同于 Kubernetes HPA 的响应式折比算法,虽然我们将资源利用率设置为目标指标,但该算法不会仅仅考虑资源利用率这一项指标,而是将历史流量(支持多条)、历史资源利用率、历史副本数都作为输入。这些指标会先通过一个线性模型,该模型能够学习这三者之间的线性关联,并得到上图中的关联函数;随后,它们会与其他信息一起(当前仅包含时间信息)通过一个残差模型,该将其他信息纳入考虑后对关联函数进行修正,能够学习到流量、容量和副本数之间的复杂非线性关联。
这里举一个简单的例子来说明残差模型的主要作用:假设某在线应用在每周日凌晨会执行一个内部定时任务,该任务会带来额外 CPU 资源消耗,但它与该应用处理的外部流量没有关联,这时候仅通过线性模型是无法学习到这一特征的。而引入残差模型后,该模型能够基于时间信息学习到该特征,因而在每周日凌晨的时间,我们给定与其他时间相同的流量和副本数,它所给出的函数会输出更高的 CPU 消耗,符合实际情况。
在目前的算法实现当中,我们使用了 ElasticNet 作为线性模型,LightGBM 作为残差模型,它们都是传统机器学习算法,不强依赖 GPU,相比于深度学习算法具有更低的使用开销,并且也能得到较好的效果。当然,你也可以根据自身的使用需求替换这些模型的具体实现,也欢迎提供你认为在某些场景下更优的实现。
在使用该模型得到关联函数之后,我们就能够把副本数预测问题转化为流量预测问题:已知目标资源利用率,只需要输入预测的流量,就能够得到(在预测流量下能够维持目标平均资源利用率的)预测的副本数。
我们设工作流信息(包含流量、资源利用率、副本数信息)为 ,目标(资源利用率)值为 ,元信息(包括时间等)为 ,我们首先使用线性模型来描绘目标函数的骨架: 随后我们计算线性模型的误差: 之后,我们将该误差和元信息通过残差模型进行修正: 最后,我们能够得到 的估计值: 其中, 和 分别可以是任意的线性和残差模型。
我们设计了一个名为 Swish Net for Time Series Forecasting 的深度学习模型来对流量指标进行时序预测,该模型专为 IHPA 的使用场景而优化,其具有下面两个主要特点:
| MAE | RMSE | |
|---|---|---|
| DeepAR | 1.734 | 31.315 |
| N-BEATS | 1.851 | 41.681 |
| ours | 1.597 | 28.732 |
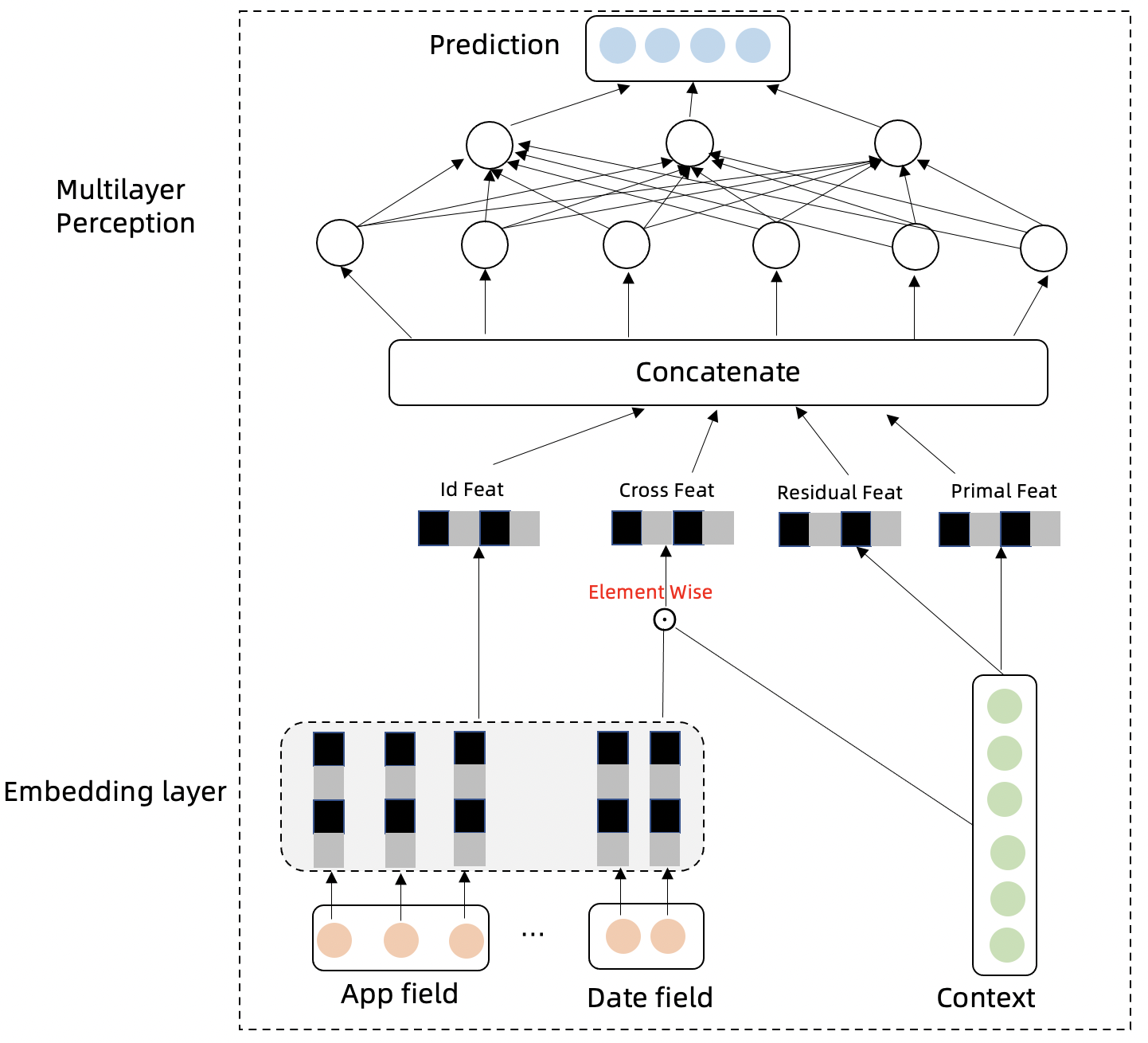
假设已经知道历史流量 ,未来真实流量为 ,预测流量为 ,流量所属的类别(如 App)为 。流量时间序列会存在周期性,趋势性,自回归特征,我们分别设计以下几个模块对这几种特性进行捕捉,并聚合信息对未来进行预测。
模型的 Embedding Layer 将类别信息和时间信息进行高维向量投射,类别信息表达不同序列的差异性,时间信息可以表达时间序列的周期性:
模型的时间特征和类别特征跟历史流量交叉特征点积可以进一步抽取不同序列的不同的差异性和周期性特征:
流量时间序列下一时间步骤与上一时间步骤的差分特征可以剔除趋势性,更好的表达时间序列的周期性,趋势性特征包含在原始序列中:
Multilayer Perception 层模型的输入以及网络结构表达如下: 多层时间网络对以上特征模块的信息进行汇总,并预测未来时间步的时间序列。
模型学习的损失函数为 MSE:
最后,我们将上述两个模型与相关数据源完整串接起来,就可以得到 IHPA 预测式扩缩容算法的完整工作流,如下图所示:

图例:
注: